辽宁仿真模拟概率有限元方法

材料优化设计是材料科学领域中的一个重要研究方向，旨在通过改变材料的组成、结构或加工方式，以实现材料的性能满足特定应用需求。随着计算机技术和数值方法的快速发展，仿真模拟在材料优化设计中扮演着越来越重要的角色。本文将探讨仿真模拟在材料优化设计中的应用、方法以及其对材料性能提升的重要性。拓扑优化设计是结构设计领域的一个重要分支，旨在通过改变结构的拓扑形态，即连接方式和布局，来优化结构的性能。近年来，随着计算机技术和数值方法的快速发展，仿真模拟在拓扑优化设计中的应用越来越流行。本文将探讨仿真模拟在拓扑优化设计中的应用、方法以及其对结构性能提升的重要性。仿真模拟外压容器稳定性分析。辽宁仿真模拟概率有限元方法

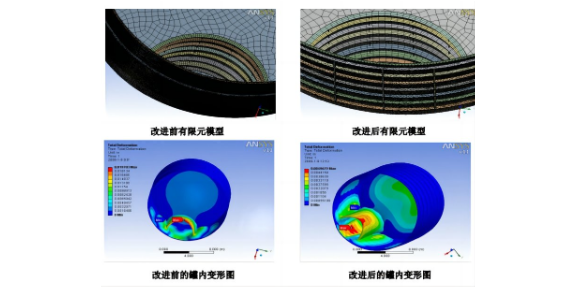
仿真模拟电-磁-热-结构多物理场耦合是一种综合分析技术，旨在模拟电场、磁场、热场和结构场之间的相互作用。在电子设备、电机、传感器等领域，这种方法对于预测和优化产品的多物理场性能至关重要，帮助工程师在设计阶段发现并解决潜在问题，提高产品的可靠性和性能。仿真模拟边界层处理是指在模拟过程中特别关注和处理流体域边界层的行为。由于边界层内流动特性复杂，包括速度梯度大、湍流强度高等特点，因此边界层处理对于准确模拟流体流动至关重要。通过精细的边界层处理，可以获得更准确的流场信息，为工程设计和优化提供可靠依据。吉林仿真模拟热分析服务商仿真模拟的未来发展趋势是什么？

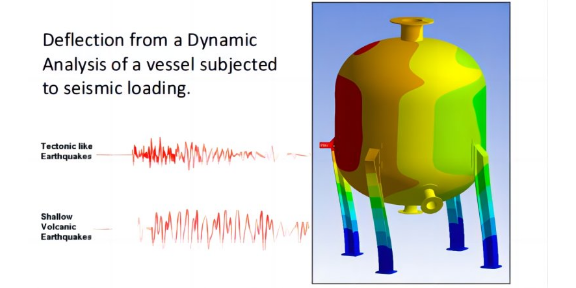
电磁-结构耦合分析的重要性体现在以下几个方面： 预测系统性能：通过仿真模拟，可以预测电磁场与结构之间的相互作用对系统性能的影响，如电磁力对结构变形的影响、结构振动对电磁场分布的影响等。这有助于工程师在设计阶段就评估系统的性能，避免潜在的问题。 优化产品设计：电磁-结构耦合分析可以帮助工程师了解电磁场与结构之间的相互作用机制，为产品设计提供指导。通过优化设计参数和结构布局，可以减少电磁场与结构之间的相互影响，提高系统的整体性能。 评估电磁安全性：在某些应用中，如电磁推进、电磁防护等，电磁场对结构的影响可能涉及安全问题。通过仿真模拟，可以评估电磁场对结构的影响是否在安全范围内，确保系统的电磁安全性。 指导实验和测试：仿真模拟电磁-结构耦合分析可以为实验和测试提供指导。通过模拟结果，可以预测实验中可能出现的问题和挑战，并制定相应的测试计划，确保实验的安全性和有效性。

静态结构分析是工程领域中一项至关重要的任务，它涉及到评估结构在静态载荷作用下的性能、稳定性和安全性。仿真模拟作为一种强大的工具，在静态结构分析中发挥着关键作用，能够帮助工程师在设计阶段预测结构的响应，优化设计方案，并减少物理测试和原型制造的成本。动态结构分析是评估结构在动态载荷（如振动、冲击等）作用下的行为和性能的关键过程。仿真模拟在这一过程中发挥着重要作用，帮助工程师预测结构的动态响应，优化设计，并评估结构的耐久性和可靠性。仿真模拟有哪些类型？探讨不同类型的仿真模拟，如物理仿真、工程仿真、经济仿真等。

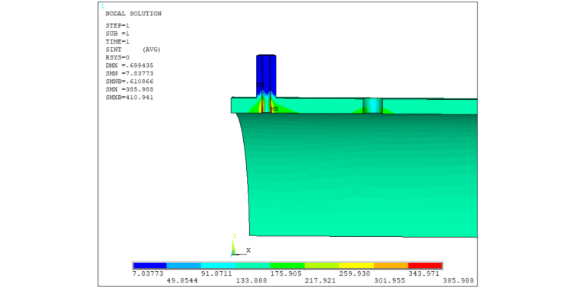
仿真模拟是一种基于数学模型和计算机技术的模拟实验方法，可以模拟复合材料的力学行为、热学行为、电磁行为等。在复合材料优化设计中，仿真模拟的作用主要体现在以下几个方面： 预测性能：通过仿真模拟，可以在设计阶段预测复合材料的性能，如强度、刚度、稳定性等。这有助于设计师在早期阶段评估和优化设计方案，减少物理试验的时间和成本。 优化设计：仿真模拟可以帮助设计师在多个设计方案中筛选出合适的方案。通过调整材料的组成、结构参数和制造工艺等因素，可以优化复合材料的性能，满足特定的应用需求。 指导制造：仿真模拟结果可以为复合材料的制造过程提供指导。例如，通过模拟材料的成型过程，可以优化制造工艺，减少缺陷和浪费，提高产品质量。讨论仿真模拟在产品设计、测试和优化过程中的重要性。辽宁仿真模拟概率有限元方法

仿真模拟如何帮助科学家在实验室环境之外探索和理解自然现象？辽宁仿真模拟概率有限元方法

疲劳分析是研究材料或结构在循环载荷作用下，由于累积损伤而导致的失效过程。疲劳分析的基本原理包括应力-寿命（S-N）曲线、Miner累积损伤准则和断裂力学等。其中，S-N曲线描述了材料或结构在不同应力水平下的疲劳寿命，Miner累积损伤准则用于计算多个应力循环下的累积损伤，而断裂力学则关注裂纹的扩展和断裂过程。铸造过程仿真模拟的意义在于，它能够在计算机上模拟铸造过程中的各种物理和化学变化，从而预测和优化铸造结果。通过仿真模拟，工程师可以在产品设计阶段就预测铸造缺陷，如缩孔、裂纹和气孔等，并采取相应的措施来避免这些问题。此外，仿真模拟还可以帮助优化铸造工艺参数，如浇注速度、浇注温度、模具温度等，以提高产品质量和生产效率。辽宁仿真模拟概率有限元方法