风电叶片疲劳试验损伤在线评估的研究

1、风电叶片疲劳加载系统 风电叶片疲劳加载系统如图 1 所示，将叶片一端 固定在塔筒上，在叶片上安装激振器对其进行激励， 使叶片产生上下摆动。在叶片主要截面上布置应变传 感器，采集加载过程中叶片表面的应变数据，用于计算疲劳损伤。

2、疲劳损伤理论和载荷许用循环次数确定 对叶片进行等幅疲劳加载时，材料承受载荷与载 荷许用循环次数之间的关系通过 S - N 曲线来描述， 如图 2 所示。金属材料的 S - N 曲线一般由试验测 定，但对于叶片的复合材料而言，试验数据较少，一般 通过经验方程描述。工程上**常用的是幂函数形式的 经验方程。

3、由 Markov 频次矩阵计算疲劳损伤 疲劳载荷历程中的每个峰谷点，都是一种特定的 载荷状态，载荷历程就是载荷状态的不断变换。利用 Markov 频次矩阵计算疲劳损伤，即求取一段载荷历 程中不同载荷循环出现的频次，并据此累计该段载荷 历程造成的总损伤。Markov 频次矩阵是一个二维方 阵，如表 1 所示，其第 i 行第 j 列的元素 nij 表示前一 次载荷为 si，后一次载荷为 sj 的情况在特定数据段中 总共出现了 nij 次。

4 、叶片载荷数据实时处理 进行风电叶片疲劳加载试验时，叶片某截面的弯 矩通过该截面的应变测量值乘以静态标定系数求得， 未经处理的弯矩波形中包含了很多噪声信号，如图 4 （a）所示。为从弯矩波形中获取弯矩峰谷值序列，须对 弯矩波形进行**小二乘二次拟合。 每次从弯矩波形中读取一段数据段 （xi，yi ）（i = 1，2，…，m），为保证拟合曲线峰谷值位置的准确性， 应满足数据长度 2 ≤ m ≤ mλ/4（mλ 为两个**近波峰 之间的数据长度）。利用二次曲线 p（x）= a + bx +cx2拟合数据段，则数据段与拟合曲线的均方误差可 表示为： Q（a，b，c）= m i = 1 Σ（p（xi ）- yi ）2 = m i = 1 Σ（a + bxi + cxi 2 - yi ）2

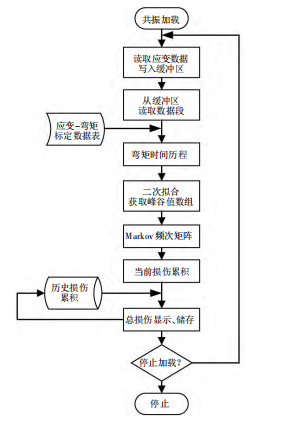
5、叶片疲劳损伤实时评估软件程序设计 采用“生产者-消费者”设计模式来实现载荷数据 的在线处理。通过 LabVIEW 和某型动态应变仪的上 位机软件共享物理内存来获得应变数据，存储在缓冲 区中。数据处理程序每隔一定时长从缓冲区中读取数 据并进行损伤计算，并将结果写入数据库。若主要截 面有 12 个，应变仪采样频率为 50Hz，数据处理程序 每隔 10 s 读取一次数据，则单次需要处理的数据量 为 6 000 个，处理时间 t ＜ 1 s，不会造成缓冲区溢出。 软件实现流程如图 5 所示。

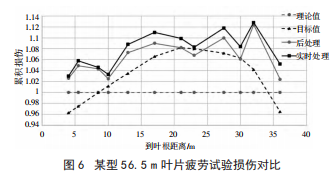
6 、实验效果 为验证风电叶片疲劳试验损伤实时评估系统的 准确性，对某型 56.5 m 叶片疲劳加载试验的损伤分 别进行实时处理和后处理，两者结果对比如图 6 所 示，图 6 中 PS 面为叶片迎风面，水平固定时朝上，SS 面为背风面，水平固定时朝下。可看出，实时处理的结 果和后处理的结果基本吻合，但各截面实时处理的结 果普遍比后者偏高 2%左右。这是由于进行后处理时， 为了提高程序运行效率，对弯矩峰峰值小于额定值 80%的数据进行了舍弃，而实时评估系统则考虑了所 有载荷造成的损伤。

结论 （1） 对风电叶片疲劳试验损伤数据进行实时处 理，每次处理的数据量非常有限，降低了对计算机运算能力的要求； （2）风电叶片疲劳试验中的载荷变化近似符合正 弦曲线，通过二次拟合后可由求导方式直接获得载荷 峰谷值，不必进行“雨流法”循环计数； （3）进行风电叶片疲劳损伤实时评估可以在疲劳 试验过程中及时获知叶片各截面损伤情况，且整个加 载周期的累计结果和载荷数据后处理的结果基本一 致，具备及时性和准确性。