风电机组叶片多点静力加载神经网络PID解耦控制

叶片静力加载系统

兆瓦级风电机组叶片全尺寸静力加载系统如图 1 所示。叶片根部通过法兰螺栓固定于加载基座上，系统采用多个节点横向加载，每个加载支架上的绞车由电液控制系统驱动，带动钢丝绳收紧或放松，对叶片进行加载或卸载，由控制算法来协调各加载节点的同步牵引。叶片静力加载系统采用的控制网络如图 2 所示。加载电液控制系统电磁换向阀改变液压马达的正反转方向，实现加载或卸载；通过调节变频器频率来改变泵的出口流量，控制各加载节点加载（卸载）的速度。控制网络采用主从通信结构。上位 PC 机与主站 PLC通过 RS485 总线进行双向通信，主站 PLC 与各加载节点从站 PLC 通过 485 总线进行轮询式双向通信，从站 PLC负责采集加载力传感器信号、与变频器通信、控制电磁阀换向动作、数据运算等，**终采集的数据反馈给上位 PC 机显示、运算、记录。

神经网络 PID 控制器设计

一、神经网络PID控制系统结构

传统 PID 通过设置比例 P、积分 I、微分 D 参数来调节系统性能，但三个参数的设定需要丰富的现场经验，并且无法适应叶片非线性强耦合等复杂多变情况。利用神经网络对 PID 参数进行在线自整定，不失为一种有效的解决方案。

所设计的多输入多输出神经网络解耦控制系统如图 3 所示。系统控制器由两部分组成：神经网络 NN：根据系统状态实时调整 PID 控制器参数，以达到期望的性能指标。

二、神经网络PID控制算法

神经网络 PID 控制算法由两部分构成：传统 PID 算法和 BP 神经网络算法。

( 一 ) 传统 PID 算法

采用离散的增量式 PID 算法

( 二 )BP 神经网络算法

BP 神经网络算法由前向传播算法和反向传播算法两部分组成。使用非负的双曲正切函数和正负对称的双曲正切函数作为 NN 网络输出层和隐含层的***函数，仍用 s 表示子网络序号，j，i，l 表示输入层、隐含层和输出层神经元序号，则在任意采样时刻 k，控制系统算法如下。

算法仿真与试验结果

试验采用n=3个节点进行加载，根据变频器频率输入控制对象液压系统到**终牵引叶片的钢丝绳拉力，结合已有的硬件参数，引入简化耦合方程(12)，模拟叶片耦合型来仿真神经网络算法的可行性。

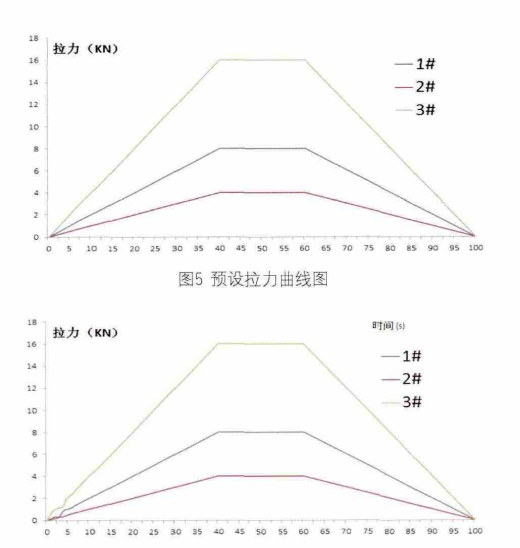
输入信号采用分段函数(13)，拉力函数曲线如图5所示。仿真时，k的单位步长取为0.5，神经网络PID算法执行周期为 0.5s间隔，系统的采样周期同样也为0.5s

设定系统三个加载节点的目标拉力值分别为8KN(1#节点)、4KN(2#节点)和16KN(3#节点)，仿真结果如图6所示。三条拉力曲线一开始出现耦合并有轻微振荡此时神经网络经过一段时间权值调整并同时调整 PID 值,此后PID趋于稳定，三个节点的拉力无振荡。由此看出神经网络具有很好的解耦控制效果，稳态误差小，响应速度快超调小。

基于本文提出的理论与仿真方案，进行了现场试验被加载叶片58.6m，进行三点加载，如图7所示。实际算法进行分工:上位机LabVIEW进行神经网络的学习算法(包括前向算法与反向算法)，下位机三个节点PLC进行传统PID 运算，得出的实际加载曲线和误差如图8、图9所示(曲线初始拉力值并非零值，因为在实际加载之前对钢丝绳进行了预紧，实际初始拉力值即为钢丝绳的预紧力)。曲线整体平滑，无***耦合现象，加载阶段误差控制在5%附近，保持阶段误差控制在1%之内，符合叶片静力加载规范要求。

结语

本文在传统PID控制算法的基础上提出了神经网络PID 控制算法，设计了神经网络PID控制器并进行了仿真与试验，发现神经网络PID控制器能够针对叶片加载多变量系统进行在线参数调整，将大幅降低耦合作用。系统动态响应好、超调小，保证了各个加载节点的牵引力同步变化。**终证明了神经网络PID算法在解决风电机组叶片多点静力加载耦合问题的可行性和有效性。